Cálculo: Explosión de la estufa de Undyne | Undertale

1

 El cálculo a continuación está basado en el de Fiction Knight que hizo ya hace tiempo, transcrito por Edgiest Femboy/Melkiades Torres. El cálculo que cito en cuestión es este de aquí.


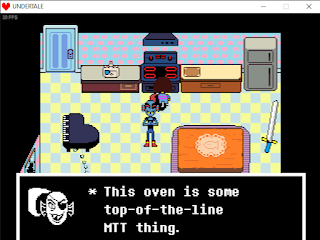
En el cálculo de Fiction Knight se asumió que la temperatura del fuego naranja sería de 1200°C, lo que sin embargo es incorrecto según la info canónica. Undyne, como se puede leer en la captura a continuación, tiene un horno de último modelo de MTT.

Esto es especialmente importante porque Mettaton nos dice de estos hornos que pueden generar hasta un pico de 9000 grados.

Teniendo esto en cuenta, repasemos la información correcta del cálculo y complementémosla con las correcciones de temperatura:

El refrigerador mide 92 píxeles, en comparación de Frisk que mide 58 píxeles. La altura promedio de un refrigerador es de 67 a 70 pulgadas (la página está caída lamentablemente), que es equivalente a 1.70 y 1,778 metros respectivamente. Teniendo eso en cuenta, Frisk mediría aprox. 1,120m, y Undyne 1,79308m.

Con esa información, podemos pasar a calcular el área de la sala de la casa de Undyne, siendo (aproximadamente) de 125,486772028 m^3.

Ahora, en lugar de usar la temperatura planteada por ellos, tomemos en cuenta que Undyne lleva la temperatura de la estufa al máximo, temperatura establecida como de 9000 grados...

Aquí hay un pequeño problema: ¿Qué unidades usaba Toby Fox cuando escribió ese diálogo?

Probablemente, Fahrenheit.
Teniendo eso en cuenta, convirtámolos a Celsius por comodidad.
Bien, tenemos que la temperatura máxima que alcanzó la estufa fue de 4982,222°C. 

Si asumimos que el dato de Fiction Knight de que el aire a esa temperatura tiene una densidad de 24kg/m^3 es correcto, además del resto de datos que trajo, el cálculo seguiría la siguiente fórmula: 

Donde:

  • Q es la energía en joules (J).​


  • m     es la masa del aire calentado (kg).

  • c es la capacidad calorífica específica del aire (J/kg·K).​


  • \Delta T     es el cambio de temperatura en kelvins (K).


Quedaría así:

Temperatura inicial del aire: 15 °C = 288,15 K
Temperatura final: 4982,222 °C = 5255,372 K
Cambio de temperatura: ΔT=5255,372K−288,15K=4967,222K

El volumen asumido por Fiction Knight fue de 1,25487 m^3, lo que se infiere porque: 1,25487m^3*24kg/m^3=30,1168kg

Resultado final:
Q=m⋅c⋅ΔT=30,1168*1012*4967,222=151.391.993,5079552‬J

En kg de TNT (porque pues, es una explosión): 151.391.993,5079552J/4184J/gTNT=36,18355485372kg de TNT.

Esto es equivalente a 151,391 Megajoules, Nivel Estructura Pequeña, pero muy superior a esos 25 megajoules calculados por Fiction Knight. Sin embargo, como se puede notar, el volumen que usó es incorrecto. No son 1.25487 m^3, si no 125.486772028 m^3, como EL MISMO CALCULÓ. Es decir, debemos hacer de nuevo el cálculo.

Masa total del aire en la escena:
125,486772028 m^3*24kg/m^3=3.011,682528672kg

Resultado final:
Q=m⋅c⋅ΔT=3.011,682528672*1012*4967,222=15.139.212.061,996411454208J

En kg de TNT (porque pues, es una explosión): 
15.139.212.061,996411454208J/4184J/gTNT=3.618.358,5234217044584627151051625kg de TNT.

15.139.212,062 Megajoules, lo cual lo dejaría en el monstruoso nivel de Pueblo Pequeño. Sin embargo, Fiction Knight por tercera vez se equivocó con otra cosa.

Tercera equivocación de Fiction Knight:

La densidad que presenta Fiction Knight de 24kg/m^3, es una sobreestimación, incluso para la temperatura que el asumió. 

La densidad del aire a temperaturas extremadamente altas, como 5000 K (aproximadamente 4727 °C), puede calcularse utilizando la ley de los gases ideales, que establece:​

ρ=pRespecıˊfico⋅T​

Donde:

  • ρ\rho es la densidad del aire (kg/m³).​

  • pp es la presión absoluta (Pa).​

  • RespecıˊficoR_{\text{específico}}es la constante específica del gas para el aire seco, aproximadamente 287.05 J/(kg·K).​

  • TT es la temperatura absoluta (K).​

Asumiendo una presión atmosférica estándar de 101325 Pa y una temperatura de 5000 K:​

ρ=101325287,05⋅5000≈0,0706 kg/m3\rho = \frac{101325}{287.05 \cdot 5000} \approx 0,0706 \, \text{kg/m}^3

Este cálculo indica que la densidad del aire a 5000 K es aproximadamente 0,0706 kg/m³, lo que es significativamente menor que la densidad del aire a temperatura ambiente (~1,225 kg/m³). Este resultado es coherente con la ley de los gases ideales, que predice una disminución de la densidad con el aumento de la temperatura, manteniendo constante la presión.

La densidad del aire a esa temperatura sería aproximadamente de 0,0671kg/m^3. Esto replantea todo el cálculo:

Masa total del aire en la escena:
125,486772028 m^3*0,0671kg/m^3=8,4201624030788kg

Resultado final:
Q=m⋅c⋅ΔT=8,4201624030788*1012*4967,222=42.326.713,7233316336907232J

En kg de TNT (porque pues, es una explosión): 
42.326.713,7233316336907232J/4184J/gTNT=10.116,327371733182048452007648184kg de TNT.

42326,71372333 Megajoules. Es decir, Nivel Edificio Grande.

Segunda posibilidad:

Aún cabe la posibilidad de que esos 9000 grados fueran grados celsius, así que rehagamos el cálculo con 9000 grados celsius. Los resultados serían estos:

Con la densidad de Fiction Knight:
27.430.404.471,144576kg de TNT / 114.768.812.307,3MJ, Nivel Pueblo

Con la densidad corregida:
18.329,550470182053154875717017208kg de TNT / 76.690,83916724MJ, Nivel Bloque​

Conclusión:

Escala original (errónea) de Fiction Knight: 
25.624297136MJ, Nivel Edificio Pequeño

Volumen corregido con 9000 grados Fahrenheit:
Corrección 1 (Solo temperatura): 151,391 MJ, Nivel Edificio Pequeño.
Corrección 2 (Densidad real del aire a esa temperatura): 42326,71372333MJ. Nivel Edificio Grande.

Volumen corregido con 9000 grados Celsius:
Corrección 1 (Solo temperatura): 114.768.812.307,3MJ, Nivel Pueblo
Corrección 2 (Densidad real del aire a esa temperatura): 76.690,83916724MJ, Nivel Bloque

Entradas más recientes Entradas antiguas

1 comentario

  1. Sickness011 de mayo de 2025, 11:19

    En Undertale se implica que usa el sistema imperial ya que Mettaton usa millas como medida de distancia: https://imgur.com/a/TKeH3oi

    Así que el resultado más correcto sería el que usa la densidad real del aire y grados Farenheits. Espero eso ayude.

    ResponderEliminar